At design time, the form looks and acts like any other form...

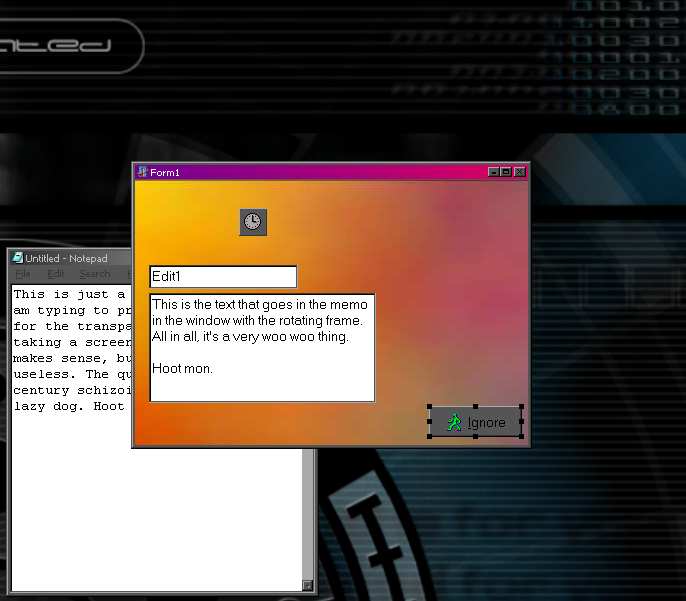
At runtime though, a timer is invoked and on each callback, the form rotates its bounding rectangle...

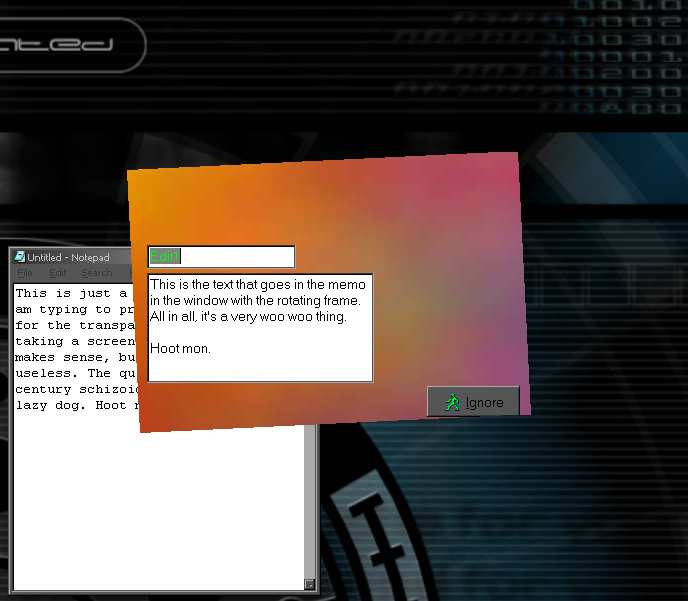
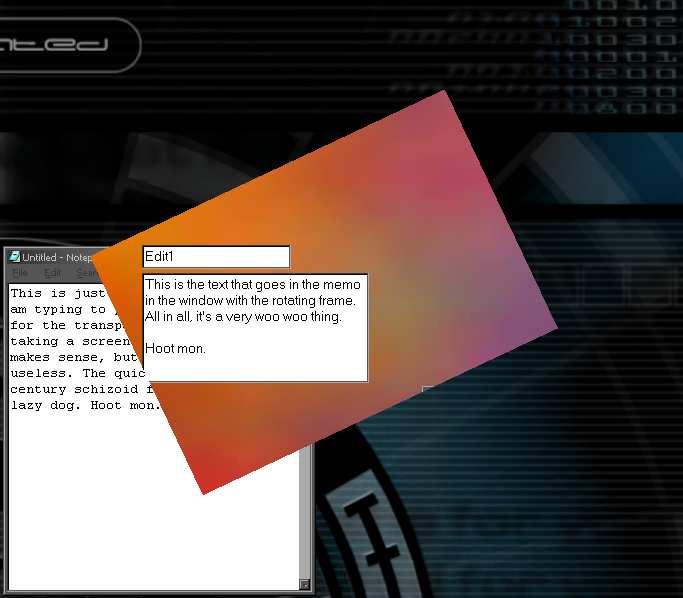
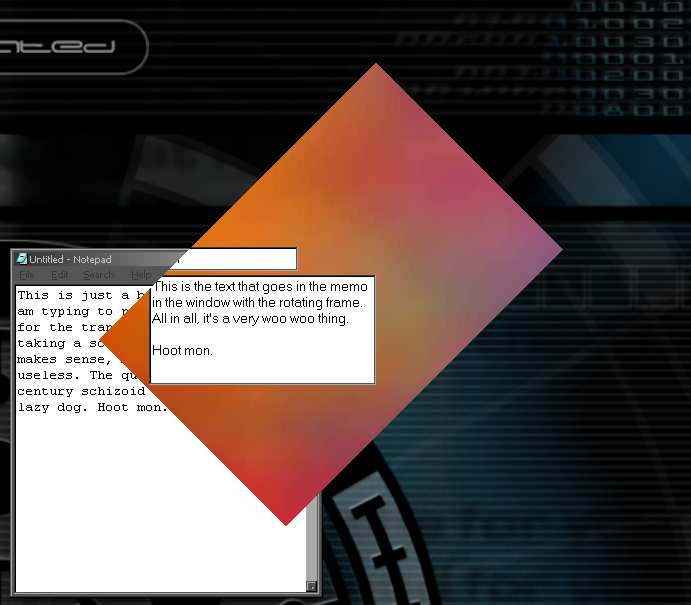
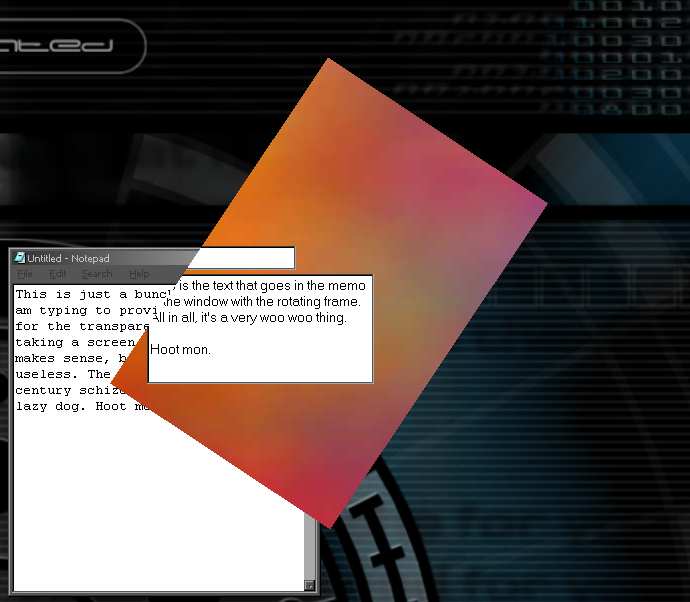
On this particular form, I have a couple of controls to emphasize that the controls are NOT moving with the form. They have a fixed (x,y,widht,height) that my code does not mess with. Also, the form has a pretty picture loaded into a TPicture, just to give something both prettier and more obviously stable than a blank gray background. (If you download the project, don't worry, the JPEG is only 8 extra k.)

I didn't bother to allow this app a way to move. That would be easy to add by putting an NC_HitTest in, or just leaving the title bar on and grabbing a portion of it as the rectangle rotates by.

Anyway, here's the important part of the code...

procedure TForm1.timTickerTimer(Sender: TObject);
  var
    point : integer;
    argn : hrgn;
    newpoly : array[0..3] of tpoint;
    minx,miny,maxx,maxy:integer;
  begin
  theta := theta + DTHETA;

  for point := 0 to 3 do
    begin
    translatepoint(apoly[point],-msx,-msy,newpoly[point]);
    rotatepoint(newpoly[point],theta,newpoly[point]);
    translatepoint(newpoly[point],msx,msy,newpoly[point]);
    end;
  argn := createpolygonrgn(newpoly,4,ALTERNATE);
  setwindowrgn(handle,argn,true);
  end;

Mostly this program is math which has nothing to do with the actual creation of regions and everything to do with making the rectangle rotate pretty.

OnCreate first saves the size and screen location of the main form. Then, in order to accomodate a rotated rectangular region that would spill beyond the form's bounds (see main clear discussion re: Windows clipping) it calculates a new larger size for the form then moves the form so that it is centered on the same place. This allows the rotating rectangle region to show fully, inside of an expanded window and appear in the place where the form was put at design time.

Since repeatedly rotating a set of coordinates like so "x := transform(x)" leads to the eventual degredation of the points, the original rectangle is also saved so that it can be rotated fresh to an absolute angle. Make the following quick hacks in the code if you want to try this yourself... (not the best code, but a quick hack)

  theta := theta + DTHETA;

  theta := {theta +} DTHETA;

  argn := createpolygonrgn(newpoly,4,ALTERNATE);
  setwindowrgn(handle,argn,true);

  argn := createpolygonrgn(newpoly,4,ALTERNATE);
  apoly := newpoly;
  setwindowrgn(handle,argn,true);

It is worth noting that when I started explaining this, I made the above changes (so I could have something to copy/paste into this HTML page) and started the program spinning. It has been running for a couple minutes now and shows no obvious degredation. I'll leave it up for a few more hours. Maybe overnight and we'll see what happens.

Right, what was I talking about? Oh yeah, the actual useful code. A new region type - polygon. Since a rectangle is necessarily parallel to X and Y axes, I needed a different kind of region to create a rotated region. Well, a rectangle is just a special polygon with four vertices. Windows allows for a polygon to specify a region. It takes a block of memory and a number of points. Easy way in Pascal, especially since I knew ahead of time that I would only need extactly and never any more and never any less than 4 points, is an array.

First, each corner vertex needs to be rotated around the center of the window/rectangle. Since simple rotate functions (like the one I use) rotate a point around the origin the points first need to be moved so that the rectangle is centered on the origin, then rotated, then moved back into normal position. This is done with the Translate-Rotate-Translate trio you see in the loop.

For a graphic explanation of what the translations fix, change...

  translatepoint(apoly[point],-msx,-msy,newpoly[point]); 
  rotatepoint(newpoly[point],theta,newpoly[point]);
  translatepoint(newpoly[point],msx,msy,newpoly[point]);

to...

  rotatepoint(apoly[point],theta,newpoly[point]);

Be careful there, that first array in rotate changes from newpoly to apoly.

Theta is the current abolute angle of rotation. DTHETA is the amount to rotate for each step. That is, if you want the rectangle to rotate at a leisurely 1 degree per tick, DTHETA=1. On the first tick, THETA==1. On the second tick, THETA==2, on the nth tick, THETA=n. Actually, I don't use degrees. I use 256ths of a circle. That way, with Theta:byte, I can just keep adding Theta:=Theta+DTHETA and it wraps around perfectly as the circle wraps around. Sine and cosine are tucked in an array calculated at initialization in the unit Trig. Look up tables are cool.

OK, that's enough rambling on about this program.

Download Project

Peter M. Gruhn